There is a one-to-one mapping between general ordered trees and binary trees. So, every tree can be uniquely represented by a binary tree. Furthermore, a forest can also be represented by a binary tree.
Conversion from general tree to binary can be done in two stages.
Stage 1:
- As a first step, we delete all the branches originating in every node except the left most branch.
- We draw edges from a node to the node on the right, if any, which is situated at the same level.
Stage 2:
- Once this is done then for any particular node, we choose its left and right sons in the following manner:
- The left son is the node, which is immediately below the given node, and the right son is the node to the immediate right of the given node on the same horizontal line. Such a binary tree will not have a right subtree.
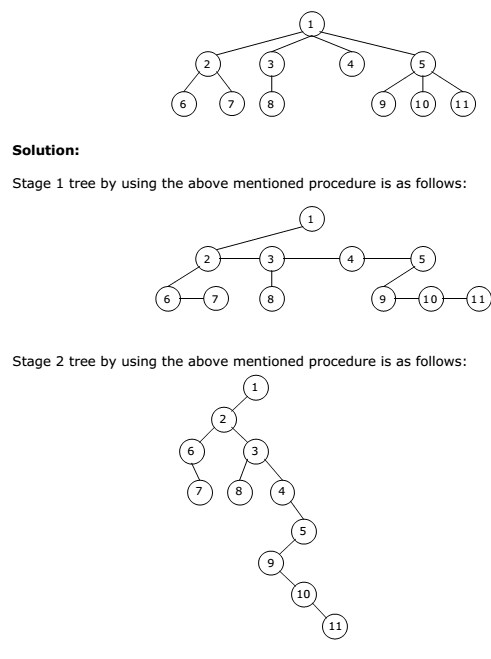
Example 1:
Convert the following ordered tree into a binary tree:
Example 2:
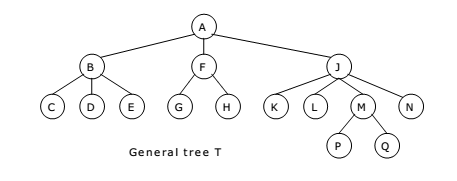
For the general tree shown below:
1. Find the corresponding binary tree T’.
2. Find the preorder traversal and the postorder traversal of T.
3. Find the preorder, inorder and postorder traversals of T’.
4. Compare them with the preorder and postorder traversals obtained for T’
with the general tree T.
Solution:
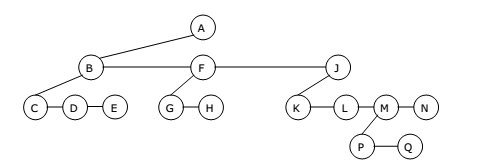
1. Stage 1:
The tree by using the above-mentioned procedure is as follows:
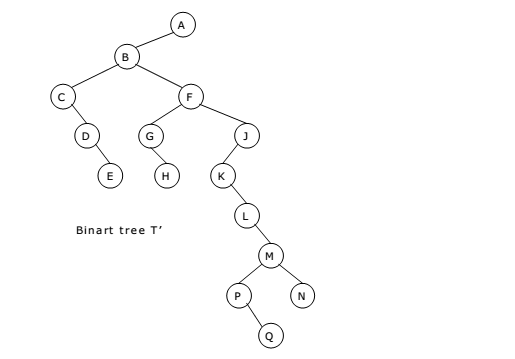
Stage 2:
The binary tree by using the above-mentioned procedure is as follows:
2. Suppose T is a general tree with root R and subtrees T1, T2, ………., TM. The
preorder traversal and the postorder traversal of T are:
Preorder:
1) Process the root R.
2) Traverse the subtree T1, T2, ……., TM in preorder.
Postorder: 1) Traverse the subtree T1, T2, ……., TM in postorder.
2) Process the root R.
The tree T has the root A and subtrees T1, T2 and T3 such that:
T1 consists of nodes B, C, D and E.
T2 consists of nodes F, G and H.
T3 consists of nodes J, K, L, M, N, P and Q.
A. The preorder traversal of T consists of the following steps:
(i) Process root A.
(ii) Traverse T1 in preorder: Process nodes B, C, D, E.
(iii) Traverse T2 in preorder: Process nodes F, G, H.
(iv) Traverse T3 in preorder: Process nodes J, K, L, M, P, Q, N.
The preorder traversal of T is as follows:
A, B, C, D, E, F, G, H, J, K, L, M, P, Q, N
B. The postorder traversal of T consists of the following steps:
(i) Traverse T1 in postorder: Process nodes C, D, E, B.
(ii) Traverse T2 in postorder: Process nodes G, H, F.
(iii) Traverse T3 in postorder: Process nodes K, L, P, Q, M, N, J.
(iv) Process root A.
The postorder traversal of T is as follows:
C, D, E, B, G, H, F, K, L, P, Q, M, N, J, A
3. The preorder, inorder and postorder traversals of the binary tree T’ are as
follows:
Preorder: A, B, C, D, E, F, G, H, J, K, M, P, Q, N
Inorder: C, D, E, B, G, H, F, K, L, P, Q, M, N, J, A
Postorder: E, D, C, H, G, Q, P, N, M, L, K, J, F, B, A
4. Comparing the preorder and postorder traversals of T’ with the general tree T:
We can observer that the preorder of the binary tree T’ is identical to the
preorder of the general T.
The inorder traversal of the binary tree T’ is identical to the postorder traversal
of the general tree T.
There is no natural traversal of the general tree T which corresponds to the
postorder traversal of its corresponding binary tree T’.
