Digital Electronics – Codes and Parity
Overview
In digital electronics, codes are used to represent information in a binary format. Parity is a technique used to detect errors in data transmission or storage.
- Binary Code: Binary code is the most fundamental form of digital code, using only two symbols: 0 and 1. It represents information using combinations of these symbols. Binary codes are widely used in digital systems for representing numbers, characters, or any other form of data.
- Parity: Parity is a simple error detection technique commonly used in digital communication and data storage systems. It involves adding an extra bit, called a parity bit, to the binary code to detect errors during transmission or storage.
- Even Parity: In even parity, the parity bit is set (1) or cleared (0) to ensure that the total number of 1s in the code, including the parity bit, is an even number. If any single bit error occurs during transmission, the parity check will detect it. However, it cannot detect errors where an even number of bits are flipped (e.g., two bits).
- Odd Parity: In odd parity, the parity bit is set (1) or cleared (0) to ensure that the total number of 1s in the code, including the parity bit, is an odd number. Similar to even parity, it can detect single bit errors but not errors where an odd number of bits are flipped.
During transmission or storage, the sender or the system adds the parity bit based on the selected parity scheme. The receiver or the system checks the received code for parity errors by counting the number of 1s. If the parity does not match the expected value, an error is detected.
Parity can provide basic error detection, but it cannot correct errors. For error correction, more sophisticated techniques like error-correcting codes (ECC) are used, which involve adding redundant bits to the code.
Parity is commonly used in applications where the probability of errors is relatively low, such as in some communication protocols, memory systems, or simple data transmission scenarios. However, in many modern systems, more advanced error detection and correction methods are employed to ensure data integrity and reliability.
BINARY CODES
In the coding, when numbers, letters or words are represented by a specific group of symbols,
it is said that the number, letter or word is being encoded. The group of symbols is called as a code. The digital data is represented, stored and transmitted as group of binary bits. This group is also called as binary code. The binary code is represented by the number as well as alphanumeric letter.
Binary-Coded Decimal Code
Binary Coded Decimal (BCD) as the name implies is a way of representing Decimal numbers in a 4 bit binary code. BCD numbers are useful when sending data to display devices for example. The numbers 0 through 9 are the only valid BCD values. Notice in the table that the binary and BCD values are the same for the numbers 0 to 9.
When we exceed the value of 9 in BCD each digit in the BCD number is now represented by a 4 bit binary value.In this code each decimal dig it is represented by a 4-bit binary number. BCD is a way to express each of the decimal digits with a binary code. In the BCD, with four bits we can represent sixteen numbers (0000 to 1111). But in BCD code only first ten of these are used (0000 to 1001). The remaining six code combinations i.e. 1010 to 1111 are invalid in BCD.
BCD Addition
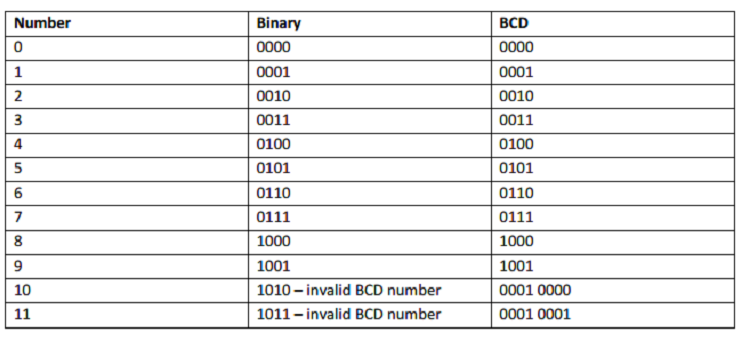
Consider the addition of two decimal digits in BCD, together with a possible carry from a previous less significant pair of digits. Since each digit does not exceed 9, the sum cannot be greater than 9 + 9 + 1 = 19, with the 1 being a previous carry. Suppose we add the BCD digits as if they were binary numbers.
Then the binary sum will produce a result in the range from 0 to 19. In binary, this range will be from 0000 to 10011, but in BCD, it is from 0000 to 1 1001, with the first (i.e., leftmost) 1 being a carry and the next four bits being the BCD sum. When the binary sum is equal to or less than 1001 (without a carry), the corresponding BCD digit is correct. However, when the binary sum is greater than or equal to 1010, the result is an invalid BCD digit.
The addition of 6 = (0110)2 to the binary sum converts it to the correct digit and also produces a carry as required. This is because a carry in the most significant bit position of the binary sum and a decimal carry differ by 16 – 10 = 6. Consider the following three BCD additions:
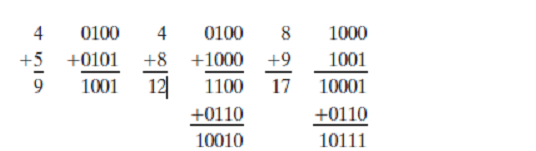
In each case, the two BCD digits are added as if they were two binary numbers. If the binary sum is greater than or equal to 1010, we add 0110 to obtain the correct BCD sum and a carry. In the first example, the sum is equal to 9 and is the correct BCD sum. In the second example, the binary sum produces an invalid BCD digit. The addition of 0110 produces the correct BCD sum, 0010 (i.e., the number 2), and a carry.
In the third example, the binary sum produces a carry. This condition occurs when the sum is greater than or equal to 16. Although the other four bits are less than 1001, the binary sum requires a correction because of the carry. Adding 0110, we obtain the required BCD sum 0111 (i.e., the number 7) and a BCD carry.
The addition of two n‐digit unsigned BCD numbers follows the same procedure.
Consider the addition of 184 + 576 = 760 in BCD:
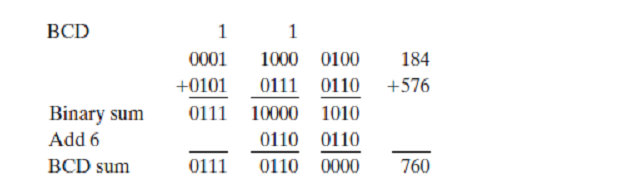
The first, least significant pair of BCD digits produces a BCD digit sum of 0000 and a carry for the next pair of digits. The second pair of BCD digits plus a previous carry produces a digit sum of 0110 and a carry for the next pair of digits. The third pair of digits plus a carry produces a binary sum of 0111 and does not require a correction.
Advantages of BCD Codes: It is very similar to decimal system. We need to remember binary equivalent of decimal numbers 0 to 9 only.
Disadvantages of BCD Codes: The addition and subtraction of BCD have different rules. The BCD arithmetic is little more complicated. BCD needs more number of bits than binary to represent the decimal number. So BCD is less efficient than binary.
Gray Codes
It is the non-weighted code and it is not arithmetic codes. That means there are no specific weights assigned to the bit position. It has a very special feature that has only one bit will chang e, eachtime the decimal number is incremented as shown in the table . As only one bit chang es at a time, the g ray code is called as a unit distance code. The g ray code is a cyclic code. Gray code cannot be used for arithmetic operation
Application of Gray code: Gray code is popularly used in the shaft position encoders. A shaft position encoder produces a code word which represents the angular position of the shaft.
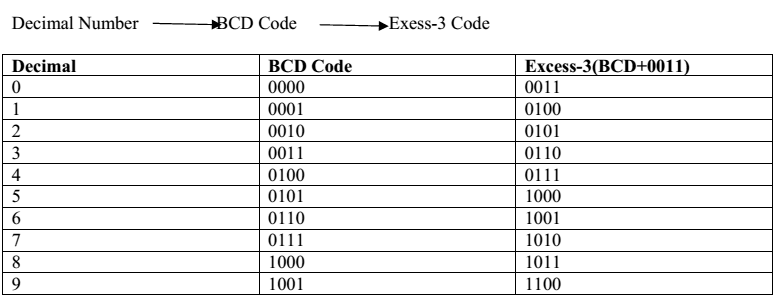
Excess-3 code
The Excess-3 code is also called as XS-3 code. It is non-weighted code used to express decimal numbers. The Excess-3 code words are derived from the 8421 BCD code words adding (0011)2 or (3)10 to each code word in8421. The excess-3 codes are obtained as follows
ASCII Code (American Standard Code for Information Interchange)
ASCII code is a 7-bit code whereas. ASCII code is more commonly used worldwide. This standard binary code for the alphanumeric characters is the American Standard Code for Information Interchange (ASCII), which uses seven bits to code 128 characters, as shown in Table given below.
The seven bits of the code are designated by b1 through b7, with b7 the most significant bit. The letter A, for example, is represented in ASCII as 1000001 (column 100, row 0001). The ASCII code also contains 94 graphic characters that can be printed and 34 nonprinting characters used for various control functions.
The graphic characters consist of the 26 uppercase letters (A through Z), the 26 lowercase letters (a through z), the 10 numerals (0 through 9), and 32 special printable characters, such as %, *, and $.
PARITY METHOD FOR ERROR DETECTION
The movement of binary data and codes from one location to another is the most frequent operation performed in digital systems. Here are just a few examples:
- The transmission of digitized voice over a microwave link
- The storage of data in and retrieval of data from external memory devices such as magnetic and optical disk
- The transmission of digital data from a computer to a remote computer over telephone lines (i.e., using a modem). This is one of the major ways of sending and receiving information on the Internet.
Whenever information is transmitted from one device (the transmitter) to another device (the receiver), there is a possibility that errors can occur such that the receiver does not receive the identical information that was sent by the transmitter. The major cause of any transmission errors is electrical noise, which consists of spurious fluctuations in voltage or current that are present in all electronic systems to varying degrees For this reason, many digital systems employ some method for detection (and sometimes correction) of errors. One of the simplest and most widely used schemes for error detection is the parity method.
Parity Bit
A parity bit is an extra bit that is attached to a code group that is being transferred from one location to another. The parity bit is made either 0 or 1, depending on the number of 1s that are contained in the code group. Two different methods are used. In the even-parity method, the value of the parity bit is chosen so that the total number of 1s in the code group (including the parity bit) is an even number.
The odd-parity method is used in exactly the same way except that the parity bit is chosen so the total number of 1s (including the parity bit) is an odd number. For example, for the code group 1000001, the assigned parity bit would be a 1. For the code group 1000011, the parity bit would be a 0. Regardless of whether even parity or odd parity is used, the parity bit becomes an actual part of the code word.
For example, adding a parity bit to the seven-bit ASCII code produces an eight-bit code. Thus, the parity bit is treated just like any other bit in the code The parity bit is issued to detect any single-bit errors that occur during the transmission of a code from one location to another.